Working with bit fields – optimize your code

Working with bit fields – optimize your code

Bitwise logical operations and packing data into bitfields is a very elementary programming technique – in fact, every microprocessor uses it internally to achieve “higher” goals like addition, subtraction, multiplication, division, and more. Nevertheless, many people who write amazing software in “high” languages are not really comfortable when it comes to bit manipulations, even if these can, as we have often seen in the Nextion Sunday Blog’s demo projects, make your code more compact, using less memory and running quicker.

Since I get more and more reader’s feedback in that sense, I decided to make a compact writeup, giving you the required knowledge at hands, not only to decipher but also to create amazing things, like for example

static inline void SPImcpDACsend(uint16_t data)
{
  MCP_DAC_CS_PORT &= ~_BV(MCP_DAC_CS_BIT);
  data &= 0x0FFF;
  data |= 0x7000;
  SPImcpDACtransmit(data);
  MCP_DAC_CS_PORT |= _BV(MCP_DAC_CS_BIT);
}

 The History

In early computing times, a long time before we got highly integrated microprocessors with a million of transistors for a few dollars, everything was built using vacuum tubes first, then transistors, before the first logic ICs in ECL, then TTL and CMOS technology emerged. The latter combined a handful of dedicated logic function blocks in an IC. Designing some simple data processing unit meant combining sometimes several tens or even hundreds of these ICs (the result was often called a TTL tomb) and routing the interconnections on a PCB (and adding decoupling capacitors) was like reorganizing a rats nest…

Then, we got microprocessors and instead of building specific hardware for an operation, we just needed to tell it to get some data from memory, load it into CPU registers, execute an operation (or more) and return the result, using a few lines of machine or assembly code:

/* 16 bit by 8 bit multiplication */
inline uint32_t mul_16_8(uint16_t a, uint8_t b) 
{
  uint32_t product;
  asm (
    "mul %A1, %2\n\t"
    "movw %A0, r0\n\t"
    "clr %C0\n\t"
    "clr %D0\n\t"
    "mul %B1, %2\n\t"
    "add %B0, r0\n\t"
    "adc %C0, r1\n\t"
    "clr r1"
    : 
    "=&r" (product)
    : 
    "r" (a), "r" (b));
  return product;
}

And today, we can let the compiler or interpreter do the work to translate our commands into machine code, it is sufficient to write c=a*b and most times, we have not longer to care of how it is done. But there are specific cases, for example if there is not much memory available or if every microsecond counts at runtime, or if we need to handle specific bits in hardware configuration registers manually, where we need that basic knowledge, thus here it is:

The Basics

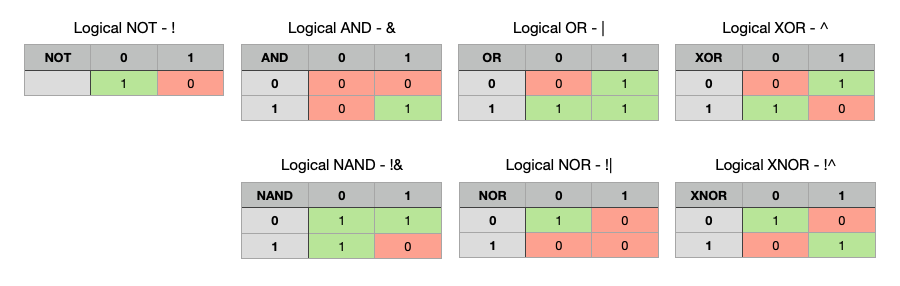
There are 4 basic logical operations: NOT (!), AND (&), OR(|), and XOR (^). These are the “grains” which allow (in parallel or sequential conjunction) to execute very complex operations, thus it is always a good idea to know these well:

r = NOT(a) or r = !a takes one input bit  and inverts it to output the result: if a is 0, r will be 1, and if a is 1, r will be 0.

r = a AND b or r = a & b takes two input bits and gives the output as follows: only if a and b are both 1, r will be 1. In all other cases, r will be 0.

r = a OR b or r = a | b takes two input bits and gives the output as follows: if either a or b (or both) are 1, r will be 1. Only if a nd b are both 0, r will be 0.

r = a XOR b or r = a ^ b takes two input bits and gives the output as follows: if exactly one of both a or b is 1, r will be 1. In all other cases, r will be 0.

Theory and practice

Often, in practice, variants of these were required for technical reasons. The most common was the N-variant where the respective output values were negated (inverted). Thus, there exist still NAND, NOR, and XNOR. They behave basically like AND, OR, and XOR, respectively, but the output value is 0 where we’d expect a 1, and 1 where we’d expect a 0.

The behavior of a logic function can be shown as a so called truth table. It allows to find the output value for any given combination of a and b:

From bits to bytes to words

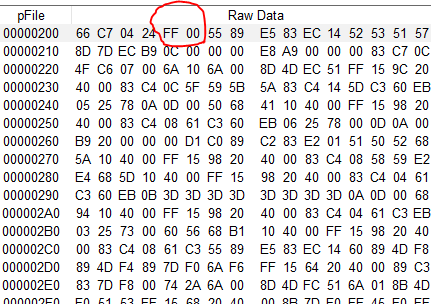
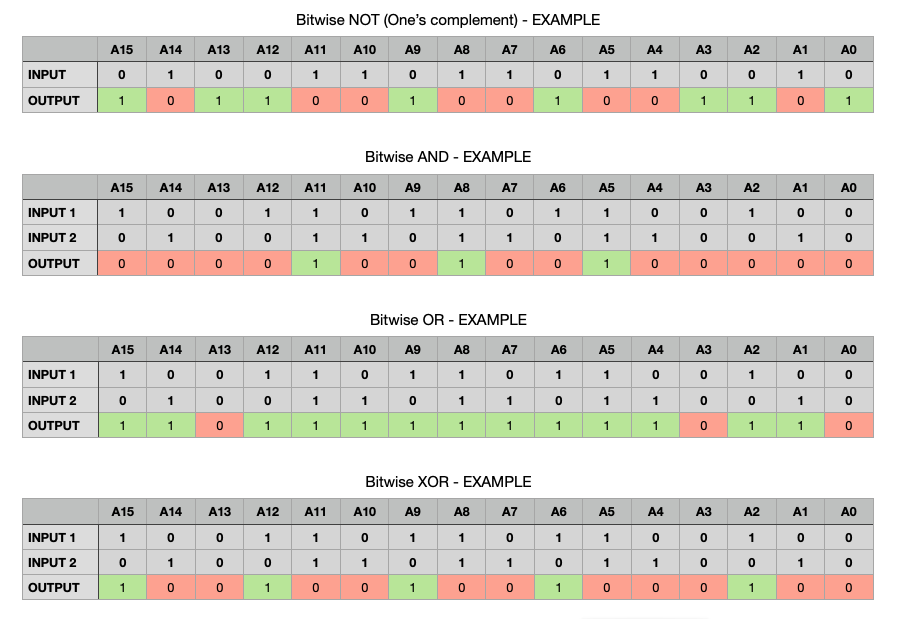
All these above functions have a huge mathematical advantage: If the one or two inputs are only one bit wide, the result or output is also only one bit wide. No need to think about overflowing or a carry bit – things that happen often with arithmetic functions or operations. That means that everything we’ve seen above applies also easily to so-called bit fields, be it a nibble (4 bits), a byte (8 bits), or a word (16, 32, or 64 bits, depending on the platform). The nth bit of the result word will be the result of the operation taking the nth bit(s) of the input value(s). When writing code in Nextion language, integer numbers are internally represented as 32bit words. Thus, coding n2.val=n1.val&n0.val will process all 32 single bits of n0 and n1 in parallel, ANDing these and write the resulting 32 bits in n2.

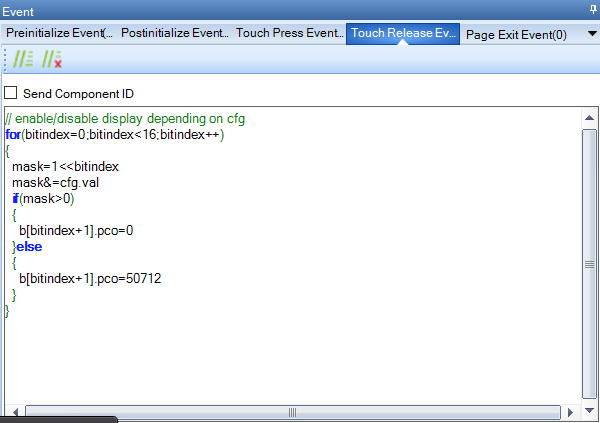
…and how does all this help to save memory?

Imagine a page with 32 dual state switches which can have a .val attribute of either 0 or 1. Thus, the status information of all 32 switches would theoretically fit into a single integer variable since it has 32 bits, one for each of the 32 switches. Storing each switch status in a separate variable would require 32 variables. Let’s save 31 of these!

In order to pack small information bits into a wider bit field, we need to address specific bits within the field. Thats where so-called bit masks come in. The simplest form of a bit mask is a “1”. As a 16bit integer for example, the representation is bit 0 = 1, bits 1 to 15 = 0. Thus, it is a bit mask for bit 0. Now, we can use the logical shift operator << to move this “1” into different places as the table below shows :

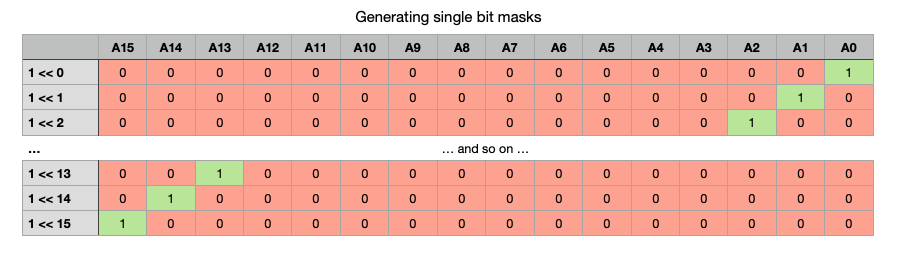
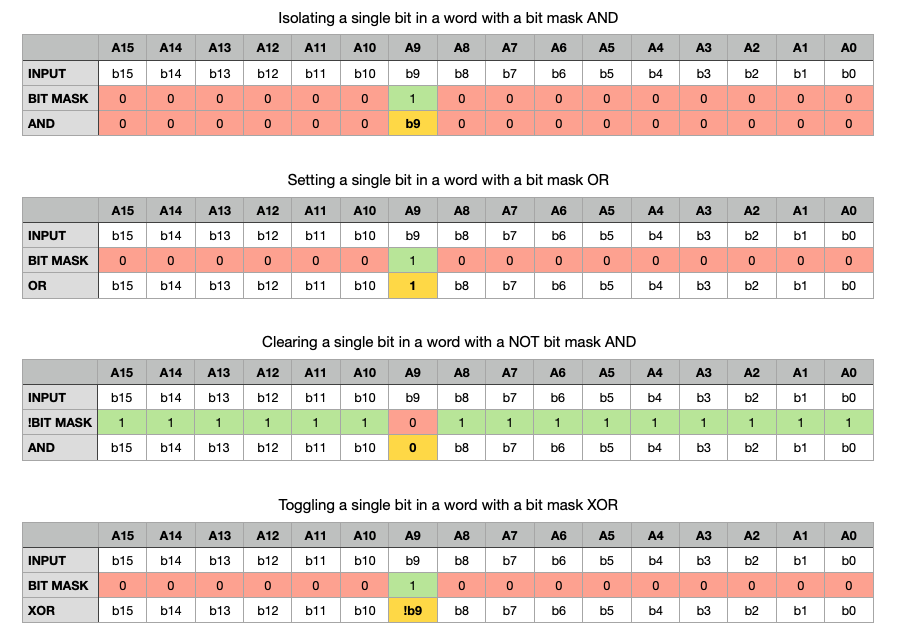
Now, using our bit mask which we generated by 1 << n to place the “1” in the nth bit position and the above logic functions and operations, we can extract or “isolate” a single bit with AND since all other result bits will be 0. Or we can set a single bit to 1 while leaving everything else unaltered with OR. We can clear a specific bit to 0 by ANDing with an inverted bit mask. And finally, we can toggle (invert) the value of a single bit while, again, leaving its neighbors unaltered:

Next time, we’ll see how we can apply our new (or refreshed) knowledge in practice to realize a 16 channel control with the famous “only a handful of code lines” 😉

For today, thank you for reading and happy Nextioning!

Questions, comments, critics, suggestions? Just send me an email to thierry (at) itead (dot) cc! 🙂

And, by the way, if you like what I write, and you are about to order Nextion stuff with Itead, please use my referral link! To you, it won’t make a change for your order. But it will pay me the one or the other beer or coffee. And that will motivate me to write still more interesting blogs 😉